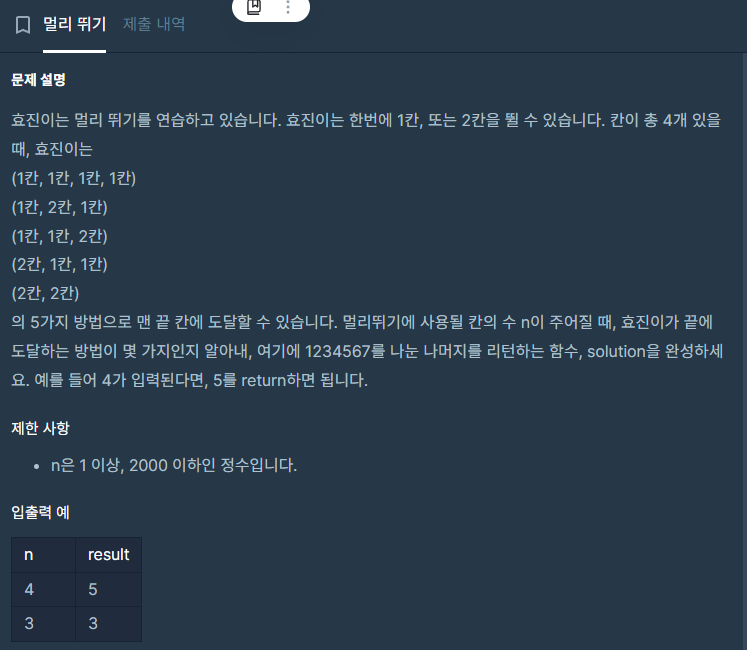
예를들어 n = 4 로 주어진다면,
(1칸, 1칸, 1칸, 1칸)
(1칸, 2칸, 1칸)
(1칸, 1칸, 2칸)
(2칸, 1칸, 1칸)
(2칸, 2칸)
이렇게 5가지 경우가 리턴된다.
| 1. 어떤 의도, 이유로 해당 기능을 구현했는지 주어진 문제에서 주어진 규칙에 따라 멀리뛰기를 할때, 마지막 위치에 도달하는 방법의 수를 계산을 하는것이 목적인데 다이나믹 프로그래밍을 활용하여 중복계산을 피하고 효율적으로 결과를 도출하려는 의도가 있습니다. 2. 해당 기능은 어떤 로직으로 코드가 작동하는지 dp 배열은 각 위치까지 도달하는 방법의 수를 저장하는 배열이다. dp[0]은 초기값으로 1로 설정되어있다. 이후, 반복문을 통해 각 위치에 도달하는 방법의 수를 동적으로 계산한다. 이중 반복문에서는 한 번에 1칸 또는 2칸을 뛸 수 있으므로 이 두 가지 경우를 고려한다. dp[i]는 이전 위치들에서 현재 위치 i로 도달하는 방법의 수를 누적한 값으로 갱신된다. 3. 버그 또는 에러 및 해결방안 코드에 에러나 버그는 없었다. |

나는 코드를 다음과 같이 작성했다.
dp라는 변수를 만들어 배열을 초기화했다. 크기가 n+1인 이유는0부터 n위치까지
도달하는 방법의 수를 배열에 저장하기 위해서다
예를들어 dp[0] 가 의미하는것은 0의 위치까지 도달하는 방법의 수 이므로 1이 될것이다.
그래서 맨처음 dp[0] = 1 로 초기화했다.
그리고 아래는 for문을 통해서 구현했다.
먼저 n은 1이상 2000이하의 정수라고 제한조건에 있다.
그래서 가장 바깥의 for문은 i를 1~n까지 잡았다.
j는 칸을 이동할때 n이 3 또는 4로 이뤄진 경우 1칸 혹은 2칸 이동하기때문에
j의 범위는 1에서 2까지 잡았다.
그래서 현재 위치에서 j만큼 뒤로 가는 것이 가능한지 확인이 필요해서
i-j >= 0 인지를 확인했다.
그 후 현재 위치까지 도달하는 방법의 수를 업데이트 했다.
예를들어 n = 4일때,
for문을 돌리면
다음과 같이 출력 해볼수 있다.
i = 1일 때,
j = 1: dp[1] = dp[1] + dp[0] (1 + 1 = 2)
j = 2: dp[1] = dp[1] + dp[-1] (j = 2일 때는 무시, 음수 인덱스는 없으므로 영향 없음)
i = 2일 때,
j = 1: dp[2] = dp[2] + dp[1] (2 + 2 = 4)
j = 2: dp[2] = dp[2] + dp[0] (4 + 1 = 5)
i = 3일 때,
j = 1: dp[3] = dp[3] + dp[2] (0 + 5 = 5)
j = 2: dp[3] = dp[3] + dp[1] (5 + 2 = 7)
i = 4일 때,
j = 1: dp[4] = dp[4] + dp[3] (0 + 7 = 7)
j = 2: dp[4] = dp[4] + dp[2] (7 + 5 = 12)
최종 결과:
dp[4]는 12가 아니라 12를 1234567로 나눈 나머지인 5가 된다.
따라서 n = 4일 때, 효진이가 끝에 도달하는 방법은 총 5가지이다.
- keep: 문제풀이가 오래걸리더라도 하나하나 디버깅하면서 방법을 찾아나가는것
- problem:생각이 복잡해 코드가 간결해지지 않는점
- try:아직 알고리즘 초짜이므로 개념(책,검색,강의)공부와 생각을 단순화하는 연습을 진행.
'TIL > kotlin 알고리즘' 카테고리의 다른 글
| kotlin 프로그래머스 lv2 괄호 회전하기 (1) | 2024.03.06 |
|---|---|
| kotlin 프로그래머스 lv2 귤 고르기 (0) | 2024.03.05 |
| kotlin 프로그래머스 lv1 N개의 최소공배수 (0) | 2024.02.29 |
| kotlin 프로그래머스 lv1 예상 대진표 (0) | 2024.02.28 |
| kotlin 프로그래머스 lv1 카펫 (2) | 2024.02.27 |